Example
3LC3. Poisson model: patents and R&D expenditure over time (336 firms in 20
industrial classes)
The data (patents.dat) we use in this example are from Hall, Griliches and Hausman (1986), and refer to the number of patents awarded to 346 firms each year from 1975 to 1979. Hall et al (1986) were particularly interested in the effect of current and lagged research and development (R&D) expenditures on the number of awarded patents. The data were made available on the web page http://cameron.econ.ucdavis.edu/racd/racddata.html to accompany Cameron and Trivedi (1988). Our analysis differs from that of Cameron and Trivedi (1988) as we allow for clustering by SIC (level 3) as well as by firm (level 2) over time. Our rationale for this is that there are 20 Industrial Classifications (IC) in these data, too many for dummy variables without amalgamating some of them, and more importantly we expect that firms in the same IC exhibit more similar patent and R&D behaviours to each other than to firms in different ICs.
References
Bronwyn Hall, Zvi Griliches, and Jerry Hausman (1986), "Patents and R&D: Is There a Lag?", International Economic Review, 27, 265-283.
A.C. Cameron and P.K. Trivedi (1998), Regression Analysis of Count Data, Econometric Society Monograph No.30, Cambridge University Press.
Data
description
Number of observations = 1681
Number of level-2 cases (‘cusip’ = identifier for firms) = 336
Number of level-3 cases (‘ardsic’ = identifier for R&D industrial classifications) = 20
The variables are:
obsno= observation number (1-1681)
cusip = Compustat's identifying number for the firm (Committee on Uniform Security Identification Procedures number).
ardssic = a two-digit code for the applied R&D industrial classification
scisect = dummy equal to 1 for firms in the scientific sector, 0 otherwise
logk = the logarithm of the book value of capital in 1972
sumpat = the sum of patents applied for between 1972-1979.
pat = the number of patents applied for during the year that were eventually granted.
pat1 = the 1 (year) lagged number of patents applied for that were eventually granted.
pat2 = the 2 (years) lagged number of patents applied for that were eventually granted.
pat3 = the 3 (years) lagged number of patents applied for that were eventually granted.
pat4 = the 4 (years) lagged number of patents applied for that were eventually granted.
logr = the logarithm of R&D spending during the year (in 1972 dollars)
logr1 = the 1 (year) lagged logarithm of R&D spending during the year (in 1972 dollars)
logr2 = the 2 (years) lagged logarithm of R&D spending during the year (in 1972 dollars)
logr3 = the 3 (years) lagged logarithm of R&D spending during the year (in 1972 dollars)
logr4 = the 4 (years) lagged logarithm of R&D spending during the year (in 1972 dollars)
logr5 = the 5 (years) lagged logarithm of R&D spending during the year (in 1972 dollars)
The first few lines of patents.dat look like:
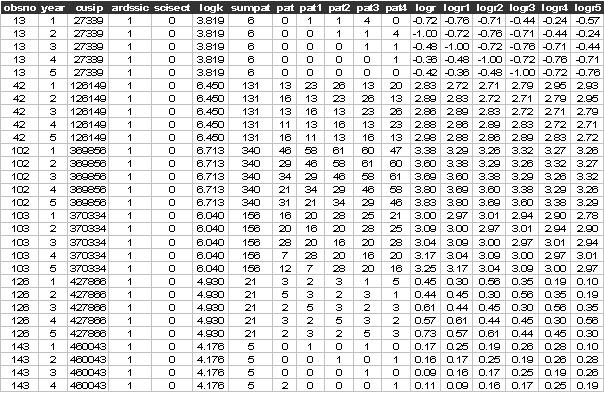
Sabre
commands
out patents.log
data obsno year cusip ardssic scisect logk sumpat pat pat1 pat2 pat3 pat4 &
logr logr1 logr2 logr3 logr4 logr5
read patents.dat
case first=cusip second=ardssic
yvar pat
family p
constant cons
factor year fyear
mass first=96 second=96
ari a
fit logr logr1 logr2 logr3 logr4 logr5 fyear logk cons
dis m
dis e
stop
Sabre
log file
<S> data obsno year cusip ardssic scisect logk sumpat pat pat1 pat2 pat3 pat4 &
<S> logr logr1 logr2 logr3 logr4 logr5
<S> read patents.dat
1680 observations in dataset
<S> case first=cusip second=ardssic
<S> yvar pat
<S> family p
<S> constant cons
<S> factor year fyear
<S> mass first=96 second=96
<S> ari a
<S> fit logr logr1 logr2 logr3 logr4 logr5 fyear logk cons
Initial Homogeneous Fit:
Iteration Log. lik. Difference
__________________________________________
1 -21734.475
2 -18762.081 2972.
3 -18671.031 91.05
4 -18670.851 0.1793
5 -18670.851 0.9293E-06
Iteration Log. lik. Step End-points Orthogonality
length 0 1 criterion
________________________________________________________________________
1 -5304.2733 1.0000 fixed fixed 163.13
2 -5295.6553 0.1250 fixed fixed 47.596
3 -5285.3719 0.1250 fixed fixed 183.49
4 -5267.5198 0.2500 fixed fixed 98.797
5 -5262.3811 0.1250 fixed fixed 41.092
6 -5250.0271 0.1250 fixed fixed 131.98
7 -5242.3925 0.5000 fixed fixed 83.603
8 -5239.5246 0.2500 fixed fixed 117.25
9 -5237.0838 0.2500 fixed fixed 126.27
10 -5231.7553 0.1250 fixed fixed 205.75
11 -5228.1188 0.1250 fixed fixed 422.83
12 -5217.5973 0.5000 fixed fixed 2372.4
13 -5140.6265 1.0000 fixed fixed 28.298
14 -5140.1334 0.0625 fixed fixed 69.417
15 -5139.7696 0.1250 fixed fixed 72.977
16 -5139.7344 0.0625 fixed fixed 22.144
17 -5135.6159 0.0625 fixed fixed 42.629
18 -5135.5317 0.0625 fixed fixed 26.594
19 -5134.6396 0.0313 fixed fixed 1121.2
20 -5120.4806 1.0000 fixed fixed 25.493
21 -5119.6906 0.0313 fixed fixed 402.63
22 -5117.0621 1.0000 fixed fixed 85.167
23 -5116.8356 0.0313 fixed fixed 33.358
24 -5116.7245 0.0156 fixed fixed 10.637
25 -5116.7083 0.0039 fixed fixed 60.915
26 -5116.6335 0.0156 fixed fixed 7.8819
27 -5116.6126 0.0020 fixed fixed 52.222
28 -5116.5142 0.0313 fixed fixed 6.2128
29 -5116.4997 0.0020 fixed fixed 35.055
30 -5116.4745 0.0078 fixed fixed 17.366
31 -5116.4626 0.0039 fixed fixed 60.681
32 -5116.4378 0.0156 fixed fixed 8.8708
33 -5116.4209 0.0020 fixed fixed 86.564
34 -5116.3791 0.0313 fixed fixed 7.4576
35 -5116.3561 0.0020 fixed fixed 43.747
36 -5116.3456 0.0156 fixed fixed 9.9933
37 -5116.3251 0.0020 fixed fixed 79.304
38 -5116.3017 0.1250 fixed fixed 8.3197
39 -5116.1818 0.0039 fixed fixed 25.815
40 -5116.1496 0.0078 fixed fixed 137.16
41 -5116.0310 0.1250 fixed fixed 6.6260
42 -5115.9642 0.0078 fixed fixed 34.590
43 -5115.9462 0.0313 fixed fixed 8.4507
44 -5115.9257 0.0039 fixed fixed 70.921
45 -5115.9079 0.0313 fixed fixed 32.974
46 -5115.8982 0.0078 fixed fixed 112.65
47 -5115.8908 0.5000 fixed fixed 599.82
48 -5115.3268 1.0000 fixed fixed 707.69
49 -5115.3255 1.0000 fixed fixed 428.38
50 -5115.3255 1.0000 fixed fixed
<S> dis m
X-vars Y-var Case-var
________________________________________________
cons pat cusip
logr ardssic
logr1
logr2
logr3
logr4
logr5
fyear
logk
Univariate model
Standard Poisson
Gaussian random effects
Number of observations = 1680
Number of level 2 cases = 336
Number of level 3 cases = 20
X-var df = 12
Scale df = 2
Log likelihood = -5115.3255 on 1666 residual degrees of freedom
<S> dis e
Parameter Estimate Std. Err.
___________________________________________________
cons -0.17569 0.62216E-01
logr 0.39203 0.38717E-01
logr1 -0.40336E-01 0.48160E-01
logr2 0.11930 0.45000E-01
logr3 0.41324E-01 0.40867E-01
logr4 0.13509E-01 0.38088E-01
logr5 0.59821E-01 0.30853E-01
fyear ( 1) 0.0000 ALIASED [I]
fyear ( 2) -0.44875E-01 0.13270E-01
fyear ( 3) -0.46142E-01 0.13457E-01
fyear ( 4) -0.17366 0.13785E-01
fyear ( 5) -0.22427 0.13901E-01
logk 0.28345 0.62823E-02
sclev2 0.89170 0.18744E-01
sclev3 0.69836 0.18762E-01
<S> stop