Example C4 Ordered response model

 

Rowan, Raudenbush, and Cheong (1993) analysed data from a 1990 survey of teachers working in 16 public schools in California and Michigan.  The schools were specifically selected to vary in terms of size, organizational structure, and urban versus suburban location. The survey asked the following question: 'if you could go back to college and start all over again, would you again choose teaching as a profession?' Possible responses were: 1 yes; 2 not sure; 3 no. We take the teachers response to this question as the response variable and try to establish if characteristics of the teachers and school help to predict their response to this question.

 

 

Reference

 

Rowan, B., Raudenbush, S., and Cheong, Y. (1993). Teaching as a non-routine task: implications for the organizational design of schools, Educational Administration Quarterly, 29(4), 479-500.

 

 

Data description

 

Number of observations (rows): 680

Number of variables (columns): 4

 

We use a subset of the data with the following:variables:

 

tcommit = the three-category measure of teacher commitment

taskvar = teachers' perception of task variety, this assesses the extent to which teachers followed the same teaching routines each day, performed the same tasks each day, had something new happening in their job each day, and liked the variety present in their work.

tcontrol = this is a school level variable, it is a measure of teacher control. This variable was constructed by aggregating nine-item scale scores of teachers within a school, it indicates teacher control over school policy issues such as student behaviour codes, content of in-service programs, student grouping, school curriculum, and text selection; and control over classroom issues such as teaching content and techniques, and amount of homework assigned.

schlid =  school identifier

 

 

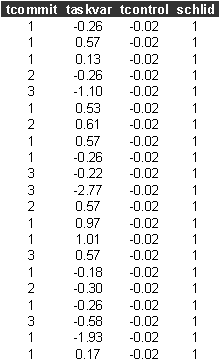
The first few lines of the teacher2.dat data set looks like

 

 

 

 

Sabre commands

 

out teacher.log

trace teacher.trace

data tcommit tcontrol schlid

read teacher1.dat

case schlid

yvar tcommit

ordered y

constant cons

lfit

dis m

dis e

fit

dis m

dis e

data tcommit taskvar tcontrol schlid

read teacher2.dat

case schlid

yvar tcommit

ordered y

constant cons

lfit tcontrol taskvar

dis m

dis e

fit tcontrol taskvar

dis m

dis e

stop

 

 

Sabre log file

 

<S> trace teacher.trace

<S> data tcommit tcontrol schlid

<S> read teacher1.dat

 

        661 observations in dataset

 

<S> case schlid

<S> yvar tcommit

<S> ordered y

<S> constant cons

<S> lfit

 

    Iteration       Log. lik.         Step      End-points     Orthogonality

                                     length    0          1      criterion

    ________________________________________________________________________

        1          -794.26611        1.0000    fixed  fixed       695.53

        2          -760.55338        1.0000    fixed  fixed       546.97

        3          -729.92355        1.0000    fixed  fixed       415.75

        4          -703.71167        1.0000    fixed  fixed       306.32

        5          -683.74061        1.0000    fixed  fixed       225.25

        6          -671.62623        1.0000    fixed  fixed       91.297

        7          -664.94055        1.0000    fixed  fixed       102.17

        8          -664.93407        1.0000    fixed  fixed       198.41

        9          -664.93407        1.0000    fixed  fixed

 

<S> dis m

 

    X-vars            Y-var

    ______________________________

                      tcommit

 

    Univariate model

    Standard ordered logit

 

    Number of observations             =     661

 

    X-var df           =     0

 

    Log likelihood =     -664.93407     on     661 residual degrees of freedom

 

<S> dis e

 

    Parameter              Estimate         Std. Err.

    ___________________________________________________

    cut1                   0.17290          0.78082E-01

    cut2                    1.1831          0.91804E-01

 

<S> fit

 

    Initial Homogeneous Fit:

 

    Iteration       Log. lik.         Step      End-points     Orthogonality

                                     length    0          1      criterion

    ________________________________________________________________________

        1          -794.26611        1.0000    fixed  fixed       695.53

        2          -760.55338        1.0000    fixed  fixed       546.97

        3          -729.92355        1.0000    fixed  fixed       415.75

        4          -703.71167        1.0000    fixed  fixed       306.32

        5          -683.74061        1.0000    fixed  fixed       225.25

        6          -671.62623        1.0000    fixed  fixed       91.297

        7          -664.94055        1.0000    fixed  fixed       102.17

        8          -664.93407        1.0000    fixed  fixed       198.41

        9          -664.93407        1.0000    fixed  fixed

 

 

    Iteration       Log. lik.         Step      End-points     Orthogonality

                                     length    0          1      criterion

    ________________________________________________________________________

        1          -668.49604        1.0000    fixed  fixed       19.308

        2          -663.21677        1.0000    fixed  fixed       64.229

        3          -662.94056        1.0000    fixed  fixed       22.566

        4          -662.75542        0.5000    fixed  fixed       40.415

        5          -662.69386        1.0000    fixed  fixed       30.343

        6          -662.66613        0.5000    fixed  fixed       36.996

        7          -662.66290        1.0000    fixed  fixed       46.090

        8          -662.66290        1.0000    fixed  fixed

 

<S> dis m

 

    X-vars            Y-var             Case-var

    ________________________________________________

                      tcommit           schlid

 

    Univariate model

    Standard ordered logit

    Gaussian random effects

 

    Number of observations             =     661

    Number of cases                    =      16

 

    X-var df           =     0

    Scale df           =     1

 

    Log likelihood =     -662.66290     on     660 residual degrees of freedom

 

<S> dis e

 

    Parameter              Estimate         Std. Err.

    ___________________________________________________

    cut1                   0.21711          0.12131

    cut2                    1.2480          0.13296

    scale                  0.33527          0.13507

 

<S> data tcommit taskvar tcontrol schlid

    --- new analysis begins

<S> read teacher2.dat

 

        650 observations in dataset

 

<S> case schlid

<S> yvar tcommit

<S> ordered y

<S> constant cons

<S> lfit tcontrol taskvar

 

    Iteration       Log. lik.         Step      End-points     Orthogonality

                                     length    0          1      criterion

    ________________________________________________________________________

        1          -781.22511        1.0000    fixed  fixed       687.60

        2          -748.47921        1.0000    fixed  fixed       555.28

        3          -718.45363        1.0000    fixed  fixed       440.45

        4          -692.12263        1.0000    fixed  fixed       344.28

        5          -670.56012        1.0000    fixed  fixed       232.94

        6          -654.29800        1.0000    fixed  fixed       28.848

        7          -634.26243        1.0000    fixed  fixed       13.519

        8          -634.05988        1.0000    fixed  fixed       10.852

        9          -634.05978        1.0000    fixed  fixed

 

<S> dis m

 

    X-vars            Y-var

    ______________________________

    tcontrol          tcommit

    taskvar

 

    Univariate model

    Standard ordered logit

 

    Number of observations             =     650

 

    X-var df           =     2

 

    Log likelihood =     -634.05978     on     648 residual degrees of freedom

 

<S> dis e

 

    Parameter              Estimate         Std. Err.

    ___________________________________________________

    tcontrol               -1.5410          0.36060

    taskvar               -0.34881          0.87745E-01

    cut1                   0.19283          0.80942E-01

    cut2                    1.2477          0.95459E-01

 

<S> fit tcontrol taskvar

 

    Initial Homogeneous Fit:

 

    Iteration       Log. lik.         Step      End-points     Orthogonality

                                     length    0          1      criterion

    ________________________________________________________________________

        1          -781.22511        1.0000    fixed  fixed       687.60

        2          -748.47921        1.0000    fixed  fixed       555.28

        3          -718.45363        1.0000    fixed  fixed       440.45

        4          -692.12263        1.0000    fixed  fixed       344.28

        5          -670.56012        1.0000    fixed  fixed       232.94

        6          -654.29800        1.0000    fixed  fixed       28.848

        7          -634.26243        1.0000    fixed  fixed       13.519

        8          -634.05988        1.0000    fixed  fixed       10.852

        9          -634.05978        1.0000    fixed  fixed

 

 

    Iteration       Log. lik.         Step      End-points     Orthogonality

                                     length    0          1      criterion

    ________________________________________________________________________

        1          -647.63394        1.0000    fixed  fixed       3.8222

        2          -641.05401        0.5000    fixed  fixed      0.91543

        3          -638.78637        0.2500    fixed  fixed       1.6313

        4          -637.15574        0.1250    fixed  fixed       10.879

        5          -636.22360        0.5000    fixed  fixed       10.812

        6          -634.52722        1.0000    fixed  fixed       39.359

        7          -634.06129        1.0000    fixed  fixed       60.755

        8          -634.05979        1.0000    fixed  fixed       32.072

        9          -634.05978        1.0000    fixed  fixed

 

<S> dis m

 

    X-vars            Y-var             Case-var

    ________________________________________________

    tcontrol          tcommit           schlid

    taskvar

 

    Univariate model

    Standard ordered logit

    Gaussian random effects

 

    Number of observations             =     650

    Number of cases                    =      16

 

    X-var df           =     2

    Scale df           =     1

 

    Log likelihood =     -634.05978     on     647 residual degrees of freedom

 

<S> dis e

 

    Parameter              Estimate         Std. Err.

    ___________________________________________________

    tcontrol               -1.5410          0.36060

    taskvar               -0.34881          0.87745E-01

    cut1                   0.19283          0.80942E-01

    cut2                    1.2477          0.95459E-01

    scale                  0.54780E-07      0.17659

 

<S> stop