Exercise 3LC2. Binary response model: Tower of London tests (226 individuals in 118 families)

This data set (tower1.dat) is from Rabe-Hesketh and Skrondal (2005). Rabe-Hesketh, Touloupolou and Murray (2001) estimated a multilevel cognitive performance model on 3 groups: (1) subjects with schizophrenia; (2) subject’s relatives and (3) control subjects. The Tower of London test was used to assess cognitive performance. The responses have a 3-level structure, i.e. occasion i for subject j in family k. The test was repeated at 3 different levels of difficulty. The binary response dtlm takes the value 1 if each test was completed in the minimum number of moves and 0 otherwise. The same data were used by Rabe-Hesketh and Skrondal (2005, exercise 7.2).

References

Rabe-Hesketh, S., Toulopoulou, T. and Murray, R. (2001). Multilevel modeling of cognitive function in schizophrenic patients and their first degree relatives. Multivariate Behavioral Research 36, 279-298.

Rabe-Hesketh, S., and Skrondal, A., (2005), Multilevel and Longitudinal Modelling using Stata, Stata Press, Stata Corp, College Station, Texas.

Data description

Number of observations = 677

Number of level-2 cases (‘id’ = subject identifier) = 226

Number of level-3 cases (‘famnum’ = family identifier) = 118

The tower1.dat includes the variables:

id= subject identifier

level= level of difficulty of the Tower of London test

famnum= family identifier

group= group (1:controls, 2:relatives, 3:schizophrenics)

age= subject’s age (years)

dtlm= indicator for completing the task in the minimum number of moves

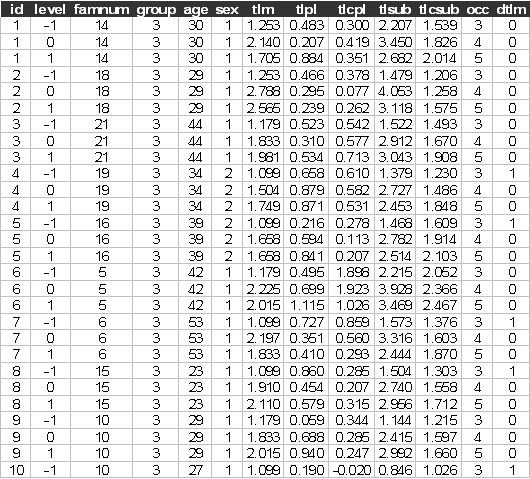
The first few lines of tower1.dat look like:

Suggested exercise:

1. Estimate a logit model (without random effects) for the binary response dtlm with the covariate level, and dummy variables for group=2 and group=3.

2. Allow for the level-2 subject random effect (id), use mass 12. Is this random effect significant?

3. Allow for both the level-2 subject random effect (id), and for the level-3 family random effects (famnum), level 3 use mass 12 for both levels. Are both these random effects significant? Is this model a significant improvement over the model estimated in part 2 of this exercise?

4. How did your results on group2 and group3 change when you allowed for subject (level 2) and then family (level 3) effects?