Exercise C3, binary
response model
Johnson and Albert (1999) analysed data on the grading of the same essay by five experts. Essays were graded on a scale of 1 to 10 with 10 being excellent. In this exercise we use the subset of the data limited to the grades from graders 1 to 5 on 198 essays (essays2.dat). The same data were used by Rabe-Hesketh and Skrondal (2005, exercise 5.4).
Data description
Number of observations: (rows) 990
Number of variables (columns): 16
Variables:
essay= essay identifier (1,2,…,198}
grader= grader identifier {1,2,3,4,5}
grade=essay grade {1,2,…,10}
rating= essay rate {1,2,…,10}, not used in this exercise
constant=1 for all observations, not used in this exercise
wordlength=average word length
sqrtwords=square root of the number of words in the essay
commas= number of commas times 100 and divided by the number of words in the essay
errors=percentage of spelling errors in the essay
prepos=percentage of prepositions in the essay
sentlength= average length of sentences in the essay
pass=1, if grade (5-10), 0 if grade (1-4)
grader2=1, if grader =2, 0 otherwise
grader3=1, if grader =3, 0 otherwise
grader4=1, if grader =4, 0 otherwise
grader5=1, if grader =5, 0 otherwise
The first few lines of the data (essays2.dat) look like:
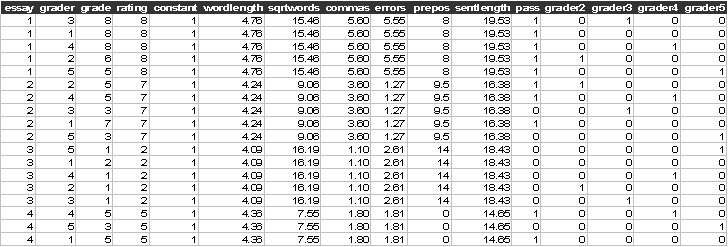
Start Sabre and specify transcript file:
out essays.log
data essay grader grade rating
constant wordlength sqrtwords
commas errors &
prepos sentlength
pass grader2 grader3 grader4 grader5
read essays2.dat
Suggested exercise:
(1) Fit a binary probit model to pass but without any random effects
(2) Fit a binary probit model allowing for the essay random effect, is the essay effect significant? How many quadrature points should we use to estimate this model?
(3) Add the 4 grader dummy variables to the model, what are the differences between the graders?
(4) Add the 6 essay characteristics to the previous model. Which of them are significant? How has including the essay characteristics improved the model?
(5) Create interaction effects between the grader specific dummy variables and the sqrtwords explanatory variable and add these effects to the model. What do the results tell you?
References
Johnson, V. E., and Albert, J. H., (1999), Ordinal Data
Modelling, Springer,
Rabe-Hesketh, S., and Skrondal, A., (2005), Multilevel and Longitudinal Modelling using Stata, Stata Press, Stata Corp, College Station, Texas