Exercise L9, bivariate linear model

Bland and Altman (1986) report on a study to compare the standard Wright peak flow meter with the (then) new Mini Wright peak flow meter. The data that accompany this study (pefr.dat) contain the repeated measurements of peak expiratory flow rate (PEFR) obtained from a sample of 17 individuals. These subjects had their PFER measured twice using the new Mini Wright peak flow meter and twice using the Standard Wright peak flow meter. To avoid instrument effects being confounded with prior experience effects, the instruments were used in random order.

Data description

Number of observations (rows): 34

Number of variables (columns): 4

Variable description:

id= person identifier

occasion=occasion {1,2}

wp=Standard Wright meter PEFR

wm=Mini Wright meter PEFR

The first few rows of the data look like:

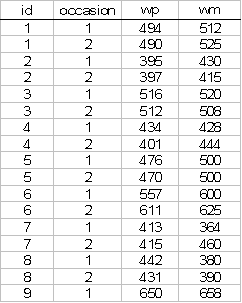
Start Sabre and specify transcript file:

out pefr.log

data id occasion wp wm

read pefr.dat

Suggested Exercise

(1) Create the dummy variable occ2, where occ2=1 if occasion =2, 0 otherwise.

Standard Wright Meter

(1) Estimate a linear model for wp with occ2 as a covariate and allowing for the id. random effect Is occ2 significant? Are the random person effects significant? Use 64 quadrature points to estimate this model?

Mini Wright Meter

(2) Estimate a linear model for wm with occ2 as a covariate and allowing for the id random effect. Is occ2 significant? Are the random person effects significant? Use 64 quadrature points to estimate this model?

Joint Model

(3) We have created a stacked version of the data (wm-wp.dat). The first few lines of this data look like:

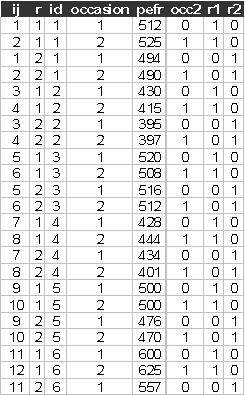
The commands to read the stacked data are:

out wm-wp.log

data ij r id occasion pefr occ2 r1 r2

read wm-wp.dat

(4) Calculate interaction effects r1_occ2 (r1 * occ2) and r2_occ2 (r2 * occ2), estimate a model for perf on r1_occ2 r1 r2_occ2 and r2, with 64 quadrature points in both dimensions. What is the significance of the correlation between the random effects of each type of meter? How does the significance of the occasion effect change when we allow for this correlation?

(5) On the basis of these data, would you be prepared to replace the Standard Wright flow meter with the new Mini Wright Meter?

References

Bland, J. M., and Altman, D., G., (1986), Statistical methods for assessing agreement between two methods of clinical measurement, Lancet, 1, 307-310.